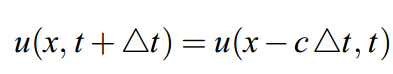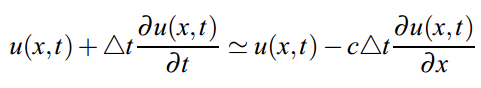移流方程式(Advection Equation) - 大人になってからの再学習

流体の学習で登場するのが移流方程式。

この移流方程式は、次のような1階偏微分方程式の形で示される。

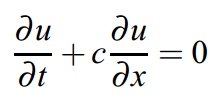
これはなんだ？？

教科書では、次のような説明が見られる。

＝＝
水にインクを落とす。すると、インクは同心円状にジワーっと広がっていく。これが拡散。
もしも、インクを落としたのが流れのある川の水面であった場合、インクは川下へ流れていく。この現象が移流。
＝＝

簡単に言ってしまえば、

「移流とは流れに沿った移動」

のこと。

何の移動なのかと言えば、インク液の濃度でもいいし、温度でもいい。何でもいい。数値で表現可能な物理量のこと。

つまり、繰り返しになるけど、移流とは

「流れに沿って物理量が移動する」

という現象のことを言う。

ここまでは、全然難しい話ではない。

左から右への流れがあれば、温度やらインクの濃度やらは、流れに乗って、左から右へ移動する。これが移流。
周りに徐々に広まって、濃度が薄くなる現象は「拡散」なので、今は考えない。拡散は無いものとする。

この「移流」の現象を、方程式という形で記述したものが「移流方程式」。

どうして、こんな形をしているんだろう？？

u というのは、何かしらの物理量を表す。繰り返しになるけど、温度だってインクの濃度だって、なんだっていい。

「この物理量を時間で偏微分したもの（第一項）と、この物理量を位置（空間）で偏微分したもの（第二項）の定数倍の和がゼロになる。」

ということを言っている。

うーん。これが、どうして「流れに沿った物理量の移動」を表しているのだろうか。

天下り式に、『「物理量が一定速度で空間を移動する」という場合に、この方程式を満たすから。そういうものだと納得してくれ。』

と説明される（または何も説明が無い）ことが多いけど、なかなか納得いかない。

これ以降、この移流方程式が、なぜこのような形をしているのか説明してみる。

まず、流れの速さは一定で、値 c で表されるものとする。

物理量 u は、時間 t と位置 x によって値が決まるので、この t と x という2変数の関数として
u (x, t)
の形で表される。

この値が、速さ c で流されていくわけだから、

観測点 x, 時刻 t における物理量 u(x, t) の値は、時刻 Δt だけ後には、位置 x+cΔt の場所に現れる。

つまり、

u(x+cΔt, t+Δt) = u(x, t)

という式で表すことができる。

後の計算のために、両方の観測点の位置を -cΔt だけずらすと、次のように表せる。

Δt が十分に小さいとすると、両辺をテイラー展開して以下の式が得られる。

これはつまり、冒頭の式

と等しい。

このようにして、「物理量が一定速度で空間を移動する」という現象を式で表すと、
冒頭に記した「移流方程式」になることを示した。

たしかに、「移流方程式」は、流れに沿って物理量が移動することを表しているのだ。

初期条件（時刻 t = 0 のときの値）が与えられれば、この方程式の解（位置と時間から求まる物理量）を求めることができる。

・参考
別の説明の仕方。上記のテーラー展開の場所が理解できない場合、こちらの方がわかりやすいかも。
http://www.waka.kindai.ac.jp/tea/shibue/1stOrderAdvectionEquation.pdf

拡散方程式の導出については、こちらが詳しい。
http://www2.kobe-u.ac.jp/~iwayama/teach/kisoIII/2011/chap6.pdf