エルミート行列

キーワード：エルミート行列、自己随伴行列、線形代数、シャルル・エルミート

エルミート行列とは何か？と言った時に次のように説明できる。

エルミート行列（自己随伴行列）→自分自身と随伴行列が等しい行列

随伴行列→転置行列の成分をすべて共役複素数に取り替えたもの

転置行列→行と列の要素を入れ替えたもの

共役複素数→虚部の符号を入れ替えたもの

以上をまとめると
「エルミート行列とは要素が複素数である行列で、行と列を入れ替えて各要素の虚部の符号を入れ替えたら自分自身に戻るもの」となる。

具体的には次のような感じ。「行と列を入れ替えて各要素の虚部の符号を入れ替える」という操作を実際に行って、もとに戻ることを確認してみよう。

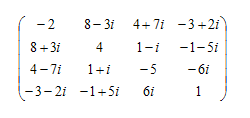
エルミート行列には次のような性質がある。
・正規行列である(逆行列がある)
・要素が実数のみであるとき対称行列となる
・固有値はすべて実数である
・異なる固有値の固有ベクトルは直交する

ではそもそもエルミート行列は、何の役に立つのだろうか？
実は数学の世界というよりも物理の世界で大いに役に立つ。
エルミート行列は量子力学の基本方程式(シュレーディンガー方程式)と密接な関係を持っている。

こんなの知っていても役に立たない、と考えるのではなくて、宇宙の原理を知るための道具の1つだ、と考えよう。

「エルミート」という言葉は、フランスの数学者「シャルル・エルミート」の名前に由来する。

シャルル・エルミートにちなんだ用語として、エルミート行列やエルミート演算子、エルミート多項式などがある。

大学数学の最初の線形代数で「エルミート行列」が出てくるあたりから、うんざりし始める学生も多いのではないだろうか。
そんなとき、その名前の由来と、その数学者の生い立ちなどをちょっと覗いてみると、無味乾燥に見える数学から、過去に生きた数学者の息づかいを感じられるようになるかもしれない。
お勧めのリンク先

・昔死んだ人（２０５）シャルル・エルミート：猫又号のブログ
・シャルル・エルミート：wikipedia
・エルミート演算子とは何か ：ＥＭＡＮの物理学・量子力学・演算子は行列だ
・エルミート行列：ときわ台学