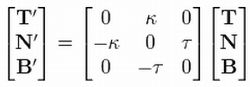フレネ・セレの公式

キーワード：フレネ・セレの公式、接ベクトル、主法線ベクトル、従法線ベクトル、曲率、捩率

3次元曲線上の点における幾何学的な性質を表すベクトルとして、下図のように3つのベクトルが定義される。

（出典：Wikipedia）

図中のT,N,Bが表すものはそれぞれ次の通り。
T: 単位接ベクトル（tangent unit vector）
N: 単位主法線ベクトル（normal unit vector）（Tの微分）
B: 単位従法線ベクトル（binormal unit vector）（TとNの外積）
上記の定義から、3つのベクトルは正規直交基底をなすことが分かる。

また、曲線上の点において次の2つの値が定義される。
κ：曲率
τ：捩率（れいりつ）：平面曲線からの離れ具合を示す

上記の3つのベクトルと2つの値に値して、次の関係式が成り立つ。

これが、微分幾何の分野で曲線を学習する時に、最初に出てくるフレネ・セレの公式（Frenet–Serret formulas）。
3つの直交ベクトルと、曲がり具合を表す2つの値が綺麗な関係で表される。

フレネ・セレの公式から、弧長sをパラメータとした曲率κ(s)と捩率τ(s)が与えられると、空間曲線を決定することができる。そのため、曲線の構造方程式とも呼ばれる。
（2次元の場合は、曲率κ(s)が与えられるだけで、平面曲線が決定される。例えば、自動車に、走行距離に応じたハンドルの回転角度を定義すれば走行軌跡が一意に定まる。と言うこともできる。）

■参考
・Frenet–Serret formulas（Wikipedia）
・ベクトル解析（Shun.Ohtani）
・フレネ＝セレの公式（物理のかぎしっぽ）

曲線と曲面の微分幾何

微分幾何 (応用数学基礎講座)