4次元の立方体の理解
「4次元の・・」という言葉を見ただけで、ああ、もう理解できるわけがない、と拒絶反応を起こすのが普通かもしれない。
でも、そんなに難しく考える必要はない。
0次元の点、1次元の線、2次元の平面、3次元の立体、と1つずつ次元を上げて行って、もう一つ次元を追加すると4次元になる。
もう1つの次元に、「時間軸」を与える話もあるけど、ここではそうではなく、あくまで幾何学的な「かたち」に関する次元とする。
この4次元の「かたち」を想像するのは難しい。
私たちは、3次元のかたちしか見たことがないのだから。
でも、どのような「構造」をしているかを想像することはできる。
0次元から3次元までの「点」「線」「正方形」「立方体」という、基本的な図形について、その構造を「頂点」「辺」「面」「胞(ほう)」に着目してまとめてみると次の表のようになる。
(※「胞」という言葉は普段見慣れないけれど、平面に囲まれる空間のこと。英語ではCell。中と外が区別できる3次元の立体は、1つの胞だと言える。)
| 次元 | 頂点の数 | 辺の数 | 面の数 | 胞の数 |
|---|---|---|---|---|
| 0次元 (点) | 1 | |||
| 1次元 (線) | 2 | 1 | ||
| 2次元 (正方形) | 4 | 4 | 1 | |
| 3次元 (立方体) | 8 | 12 | 6 | 1 |
このように表にまとめてみると、その規則性が見て取れる。
その規則を使うと、もう一つ上の次元、4次元の立方体の構造が予想できる。
4次元の立方体のことを「超立方体」と呼ぶ。
これを追加した表は次の通り。
| 次元 | 頂点の数 | 辺の数 | 面の数 | 胞の数 |
|---|---|---|---|---|
| 0次元 (点) | 1 | |||
| 1次元 (線) | 2 | 1 | ||
| 2次元 (正方形) | 4 | 4 | 1 | |
| 3次元 (立方体) | 8 | 12 | 6 | 1 |
| 4次元 (超立方体) | 16 | 32 | 24 | 8 |
■ 頂点の数は2倍ずつ増える
0次元は頂点1つ。1次元の場合は(±1)で2つ、2次元の場合は(±1,±1)で4つ、3次元の場合は(±1,±1,±1)で8つ。このようにして4次元では4次元座標(±1,±1,±1,±1)の16個が頂点となる。
■ 辺の数は1つ前の次元の「辺の数の2倍と頂点の数」を足した数になる。
もとのカタチを新しい次元に平行移動して(辺の数は2倍増える)、対応する頂点間を結ぶため(辺の数は頂点の数だけ増える)。
下の図がわかりやすい。

■ 面の数も同じように考えて、1つ前の次元の「面の数の2倍と辺の数」を足した数になる。
このようにして、4次元の立方体、つまり「超立方体」の構造がわかった。
4次元の超立体の16個の頂点は、4次元座標(±1,±1,±1,±1)で表され、辺は最も近い距離にある点通しを結ぶ位置に存在する。
では、このような性質を持つ超立方体はどのような形をしているのだろうか。
残念ながら、私たちは4次元のかたちを直接「見る」ことはできないし、頭の中に想像することも難しい。
でも、3次元の立体を平面に投影することで、立体を2次元の図として見ることができるように、
4次元の立体も3次元の平面に投影することで、3次元の立体として見ることができる。
パソコンの画面で表示するにはさらに次元を落として2次元の図にする必要があるけど、2次元の図から3次元のかたちを想像するのはたやすいのであまり心配はない。
さて、その結果として、次のような図が得られる。
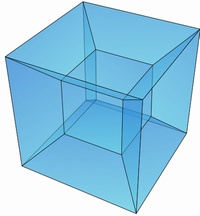
この形は4次元のかたちを、ある方向から投影した結果の3次元のかたちなので、
当然、投影の方向によって結果が異なる。
ある立体の影の形が光の方向によって異なるように、4次元のかたちを見る方向によって3次元のかたちは変化する。
その変化の様子を表すアニメーションが WikiPedia に紹介されている。
http://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:8-cell-simple.gif

4次元座標で表された図形を3次元に投影するアルゴリズムについて、こちらで紹介されている。
http://steve.hollasch.net/thesis/chapter4.html
もう「4次元の・・」と言われても、そんなに恐れる必要はない。
参考:
http://en.wikipedia.org/wiki/Four-dimensional_space

- 作者: おまけたらふく舎
- 出版社/メーカー: 誠文堂新光社
- 発売日: 2011/05
- メディア: 単行本
- クリック: 1回
- この商品を含むブログを見る

幾何学の不思議:遺跡・芸術・自然に現れたミステリー (アルケミスト双書)
- 作者: ミランダ・ランディ,駒田曜
- 出版社/メーカー: 創元社
- 発売日: 2011/04/21
- メディア: 単行本
- クリック: 1回
- この商品を含むブログ (2件) を見る