重心座標系（Barycentric coordinate system） - 大人になってからの再学習

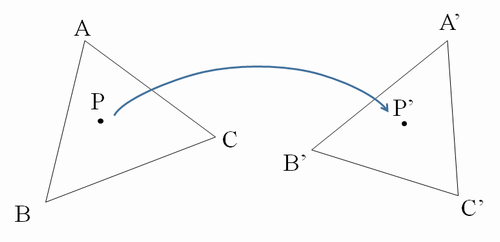
三角形ABC内の点Pを、別の三角形A'B'C'内の、それっぽい場所P'に対応させたい。
P'の位置はどのように決めたらいいだろうか。

それっぽい場所。。って、曖昧すぎる。

そこで、重心座標系（Barycentric coordinate system）が用いられる。

三角形ABC内の任意の点Pの座標は、

P=αA+βB+γC

の形で表現できる。
つまり、三角形の各頂点座標の線形和。
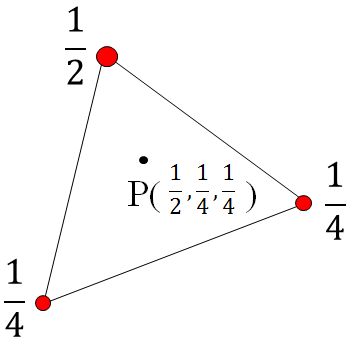
3つの係数だけで位置が決まるので、

P=(α，β，γ）

という形で表現することができて、
これを重心座標と言う（重心の座標ではなくて、重心座標系で表した時の座標値ということ）。

三角形の3つの頂点を参照して位置を決める方法なので、

P'＝αA'+βB'+γC'

とすれば、三角形ABC上の点Pと、三角形A'B'C'上の点P’をうまく対応付けすることができる。
（三角形ABC上全体が、三角形A'B'C'全体に1対1対応する）

では、重心座標（α,β,γ）は、どのように算出されるだろうか。

2次元図形の三角形内の座標を表すのに、変数は3つもいらないので、

α＋β＋γ＝１

として

γ＝１−αーβ

と表す。

点A,B,Cのx,y座標をそれぞれAx,Ay,Bx,By,Cx,Cyとし、点Pの座標をPx,Pyとすると、α,β,γは次の式で求められる。

α＝{(By-Cy)(Px-Cx)+(Cx-Bx)(Py-Cy)}/{(By-Cy)(Ax-Cx)+(Cx-Bx)(Ay-Cy)}
β＝{(Cy-Ay)(Px-Cx)+(Ax-Cx)(Py-Cy)}/{(By-Cy)(Ax-Cx)+(Cx-Bx)(Ay-Cy)}
γ＝１−αーβ

α,β,γの値と、それに対応する点には次の関係がある。

・三角形内部の点はα、β、γの値がすべて0と1の間に収まる。
・いずれかの値が0のとき、三角形の辺上の点となる。さらに、いずれの値が1であれば、三角形の頂点に重なる。
・上記以外の場合（0より小さいまたは1より大きい値がある場合）は三角形の外側の点となる。

ちなみに、重心座標系という名前がついている理由は、各点にα、β、γの重さの点を置いた時の重心が点Pになるため。

ここで示したのは代表的な例で、2次元である必要はないし、図形が三角形である必要もない。