ボイヤー・ムーア法 - 大人になってからの再学習

文字列の検索アルゴリズムとして、ボイヤー・ムーア法と呼ばれる有名なものがある。

詳しくはWikipediaの「ボイヤー-ムーア文字列検索アルゴリズム」を見てもらうとして、直観的に理解するには次のページの図がわかりやすい。

■ [ITpro http://itpro.nikkeibp.co.jp/article/MAG/20061115/253802/:title=こうしろうのMindStorms日記 - 第78話　効率がいいアルゴリズムは美しい]

↓単純なマッチングによる検索

↓ボイヤー・ムーア法による検索

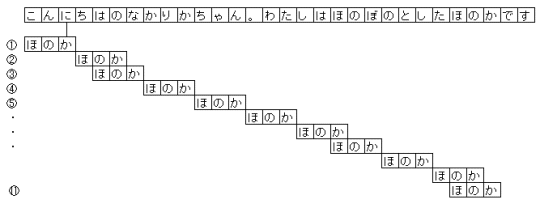
ボイヤー・ムーア法の方が、文字列の比較回数が少なくて効率がよいことがわかる。

ところで、今回のエントリの本題はこの文字列検索のボイヤー・ムーア法ではなくて、ボイヤー・ムーアの過半数判定アルゴリズムの話。

ボイヤー・ムーア法と言うと文字列検索の「Boyer-Moore String Search Algorithm」が有名だけど、実は「Boyer-Moore Majority Vote Algorithm」と言うものもある。こちらはとてもマイナーらしい。

これは「投票結果から過半数の票を獲得した候補者がいるか、もしいるのであれば、それは誰か」という判定を効率的に行うアルゴリズム。

具体例として、A,B,Cの候補者がいて、次のように投票された場合を考えよう。

A A A C C B B C C C B C C

A,B,Cそれぞれの票の獲得数は次の通り。
A：3票
B：3票
C：7票
票の数は全部で13票なので、Cは過半数を獲得している。

次の場合はどうだろうか。

A A A (B) C B B C C C B C C

カッコの部分がCからBに変わった。
その結果、それぞれの獲得数は次のようになる。
A：3票
B：4票
C：6票
票の数は全部で13票なので、Cは過半数の獲得には失敗した。つまり、過半数を獲得した候補者はいない、ということになる。

単純に考えれば、1つ1つ投票の内容を確認して、投票された候補者のカウンタを1だけ増やせばいい。簡単な問題だ。
でも、この方法だと候補者の数だけカウンタを準備しておく必要がある。
候補者が10万人いたら、10万の変数が必要になる。
ありえない話だし、もし実際にあっても最近のパソコンだったら問題なさそうだけど、
変数はたった2つだけで済むよ。、計算時間も線形時間だよ、というのがボイヤー・ムーアの過半数判定アルゴリズム。

1つの変数eで、過半数を獲得する可能性のある候補者を記憶する。
もう1つの変数cは、カウンタの値を記憶する。

実際のアルゴリズムは、投票内容を格納する配列を先頭から末尾に向かって1つずつ参照しながら、次のように候補者を決定する。
・カウンタcが0の場合は、過半数獲得の候補として変数eに現在参照している票の内容を格納する。
・カウンタcの値が0でない場合は、現在参照している票の内容が変数eと一致する場合にcの値を1増やし、そうでない場合は1減らす。カウンタが0になったらeをリセット。

たったこれだけのアルゴリズムで、最終的に変数eに格納されている内容が、過半数を獲得する可能性のある候補者になる。
つづいて、この候補者への投票数が実際に過半数を占めているかどうかを投票内容の配列を再確認して判定する。
つまり、配列の先頭から末尾に向かっての全要素の参照は2回行われることになる。

ここで、注意したいのは、過半数を獲得する候補者が存在しない時、「最終的に変数eに格納される要素は、最もたくさんの票を獲得した候補者であるとは限らない」という点。
これはとてもユニークだ。

このアルゴリズムがどのように動作するのか、最初に挙げた例で見てみよう。初期段階ではeは未定、cは0だ。これを(?, 0)の形で末尾に記すものとする。

初期状態