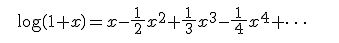log(1+x)のテイラー展開・マクローリン展開
昨日のエントリ「70の法則、72の法則」の中で、xの値が十分小さいときに次の式が成り立つ、ということを書いた。
なぜなのか疑問に思うかもしれないので、簡単に説明する。
無限回微分可能な関数f(x)について、次式が成り立つ。これをf(x)のx=aでのテイラー展開と言う。
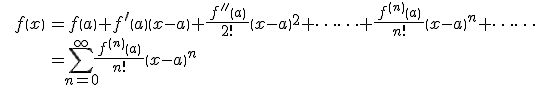
a=0としたものをマクローリン展開とよび、次のように表せる。

をマクローリン展開すると、次のようになる。
(どうしてこのように展開されるかは次を参照: log(1+x) のマクローリン展開の導出(KIT Mathematics Navigation))
今回、xの値が十分に小さいとしているので、2次以降の項を無視すれば
となる。
仮に、x=0.02 とした場合(昨日のエントリ「70の法則、72の法則」の中での金利2%のケースに相当)、 実際の値はlog(1+x)=log(1.02)=0.019802.. であるため、かなり正確な近似であることがわかる。
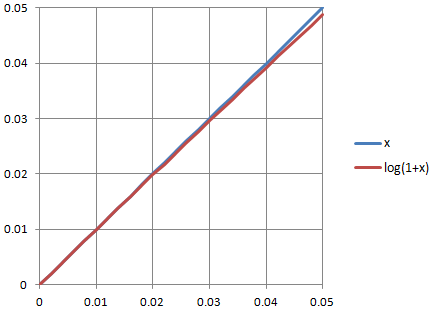
0.05までのy=xとy=log(1+x)のグラフは次の通り。ほぼ一致していることを視覚的にも確認できる。

- 作者: 矢野健太郎,石原繁
- 出版社/メーカー: 裳華房
- 発売日: 1991/12/01
- メディア: 単行本
- 購入: 5人 クリック: 32回
- この商品を含むブログ (4件) を見る

- 作者: 石村園子
- 出版社/メーカー: 共立出版
- 発売日: 1999/12/01
- メディア: 単行本
- 購入: 6人 クリック: 145回
- この商品を含むブログ (17件) を見る